Bernoulli’s Principle is one of the most important concepts in fluid dynamics and plays a crucial role in the operation of pumps and many other hydraulic systems. Developed in the 18th century by the Swiss mathematician and physicist Daniel Bernoulli, this principle describes the relationship between velocity, pressure, and potential energy of a flowing fluid. On this content page, we take a closer look at Bernoulli’s Principle, its mathematical formulation, applications in pump technology, and the practical implications for engineers and technicians.

Bernoulli’s Principle states that in the flow of an ideal fluid, the sum of kinetic energy, potential energy, and pressure energy per unit volume remains constant along a streamline. This principle can be expressed mathematically as:

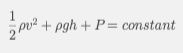
where:

ρ is the density of the fluid,
v is the velocity of the fluid,
g is the acceleration due to gravity,
h is the height above a reference level,
P is the pressure in the fluid.

This equation implies that an increase in fluid velocity results in a decrease in pressure or potential energy, and vice versa. This phenomenon is at the core of many hydraulic and aerodynamic applications.

The IPG team of dedicated pump experts is ready to support you.
Call us on business days between 08:00 and 18:00.

Tel: +31(0251) 222 566

Bernoulli’s Principle is particularly important in the design and analysis of pumps. Below are several ways in which this principle is applied:

1. Velocity and Pressure Changes in Pump Impellers
In a centrifugal pump, the impeller increases the velocity of the fluid. According to Bernoulli’s Principle, this increase in velocity leads to a reduction in pressure near the impeller blades. This concept helps engineers understand how pressure distribution around the impeller changes and how it affects pump performance.

2. Cavitation Prevention
Cavitation, the formation of vapor bubbles in a liquid, occurs when the pressure in the fluid drops below its vapor pressure. Bernoulli’s Principle helps predict locations within a pump system where pressure may become low enough to cause cavitation. By carefully analyzing flow conditions, engineers can design systems that prevent cavitation and extend pump service life.

3. Pipe Diameter and Flow Velocity
When transporting fluids through piping systems, it is essential to understand how changes in pipe diameter affect velocity and pressure. According to Bernoulli’s Principle, a reduction in pipe diameter results in higher velocity and lower pressure. This knowledge is used to select optimal pipe diameters throughout a system to ensure efficient operation.

The following examples illustrate how Bernoulli’s Principle is applied in real-world situations:

1. Firefighting Hydrants
In firefighting hydrants and other emergency water supply systems, fast and efficient water flow is critical. Bernoulli’s Principle allows engineers to calculate how changes in pipe diameter and elevation affect water pressure and velocity. This supports the design of systems that respond quickly in emergency situations.

2. Cooling Systems in Electronic Equipment
In cooling systems for electronics such as computers and other sensitive equipment, coolant must flow efficiently through narrow channels. Bernoulli’s Principle helps predict flow behavior, which is essential to avoid hotspots and ensure uniform cooling.

3. Medical Equipment
In medical applications such as infusion pumps, precise control of fluid flow is essential. Bernoulli’s Principle helps explain how pressure differences can be used to maintain a constant and controlled flow rate, which is critical for patient safety and treatment effectiveness.

For engineers and technicians working with pumps and fluid systems, a solid understanding of Bernoulli’s Principle is essential. Key implications include:

1. Design and Optimization
When designing pumps and piping systems, Bernoulli’s Principle can be used to determine optimal configurations that maximize efficiency and minimize risks such as cavitation.

2. Troubleshooting
If a pump system does not operate as expected, Bernoulli’s Principle can help identify the root cause. For example, an unexpected pressure drop may indicate a blockage or leakage, while cavitation may result from incorrect operating parameters.

3. Training and Education
Professionals in the pump industry benefit from ongoing training and education on the latest applications of Bernoulli’s Principle and other fluid dynamics concepts. This helps ensure they remain up to date with technological developments and best practices.